前回、GNNの仕組みについて説明しました。お隣さんから情報を収集し、それらを集約して、クラスを判別・予測します。今日は、最も人気のあるGNNの1つである「GRAPH CONVOLUTIONAL NETWORKS」または「GCN」(1)について詳しく説明します。それでは始めましょう。
1.隣接行列 (adjacency matrix)
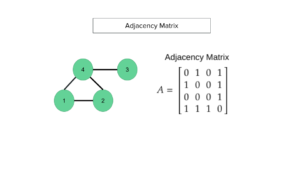
ご存知のように、グラフにはノード(交点)間にエッジ(経路)またはリンクがあります。したがって、隣接行列Aとノード特徴量Hを使用してグラフを定義できます。ノードの数をNとすると、隣接行列AはN×Nの行列になります。隣接行列は、ノード間の関係を表すのに非常に役立ちます。グラフにノード「i」からノード「j」へのリンクがある場合、行が「i」で列が「j」であるAの要素は「1」、それ以外の場合は「0」です。下のチャートに例を示します。ノードにそれ自身へのリンクがある場合、対角要素は「1」になります。一方ノード特徴量Hは、例えばカラー写真を考えるとN×3の行列になります。各ノードはRGBの3つの値を持つからです。
2.お隣さんから情報を集める
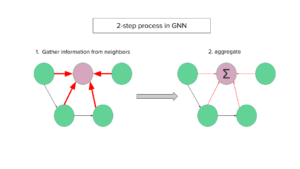
それでは下のチャートを使ってグラフがどのように情報を更新していくかをご説明しましょう。 2つのプロセスから成っています。
- グラフで赤く表示されている真ん中のノードは、お隣さんから情報を収集します。
- 集められた情報は、ノードを更新するために集約されます。集計の方法は、合計または平均を使います。
- GCN
上で述べたように、グラフは隣接行列Aとノード特徴量Hで定義できます。ここでは、隣接行列Aの対角要素は「1」とします。 次に学習可能なウエイトを示す行列としてWを導入し線形変換を施します。さらに隣接行列Aの次数行列Dを導入します(次数は各ノードに接続したエッジの数)。 σは非線形関数です。
ここでGCNの登場です。GCNでは、情報を収集する方法が上記2でご紹介したものより少し工夫されており、次のとおりです(1)。
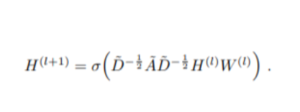
これは、お隣さんからの情報が、送信者(緑)と受信者(赤)の次数に基づいてウエイト付けされることを意味します。すべての情報は、受信者(赤)の情報を更新するために集約されます。
行列で表す上式よりも、ノード毎に記述する以下の式の方がわかりやすいかも知れませんね。送信者(緑)は 「j」 受信者(赤)は「i」で示されています。aijは送信者(緑)と受信者(赤)の次数に基づくウエイトです(2)。
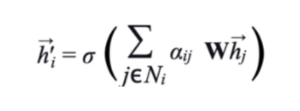
これで完了です。 GCNがどのように機能するかをご理解していただければ幸いです。次の記事では、GCNを用いて簡単な問題を解きたいと思います。ご期待下さい。
(1)SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS,Thomas N. Kipf&Max Welling、2017年2月22日
(2)Intro to graph neural networks (ML Tech Talks) , youtube, Petar Veličković、2021年6月6日


