ヒストグラムはデータ分析の基本ツールであり、データ分布を視覚的に表現します。 ただし、単純なビニング方法、不適切な使用例、モデル キャリブレーションなどの特定のアプリケーションでの落とし穴によって、その有用性が大幅に損なわれる可能性があります。 この投稿ではこれらの側面を掘り下げ、より洗練されたアプローチの必要性を強調します。
ヒストグラムの単純なビニングの危険性
ヒストグラムは非常にシンプルで理解しやすい方法なので、使用するときにヒストグラムについて考えることに多くの時間を費やす人はいません。 ただし、ビンの幅とビンの開始点の選択はヒストグラムの外観に大きく影響し、誤解を招く解釈につながる可能性があります。 たとえば、同じ幅のビンは、特にデータ分布に偏りがある場合や外れ値がある場合に、基礎となるパターンを不明瞭にする可能性があります。
ビニングに一般的に使用される方法であるスタージェス ルールは、多くのシナリオでは不十分です。 スタージェスのルールはシンプルで、小規模なデータセットに対してはかなりうまく機能しますが、大きなデータセットに対してはビンの数が過小評価されることが多く、単純化しすぎてデータの微妙なニュアンスを捉えることができないヒストグラムが生成されます。 ただし、一部のソフトウェア パッケージでは依然としてデフォルトのようであり、実生活では依然として頻繁に使用されているのを目にします。
Freedman-Diaconis ルールなどのより洗練された方法では、データの四分位範囲 (Interquantile range, IQR) とサンプル サイズに基づいてビン幅を調整します。 この方法はデータの変動性と密度に適応し、基礎となる分布をより正確に表現します。 データ ポイントの広がりと数を考慮することにより、Freedman-Diaconis ルールは、より素朴な手法でよくある過剰平滑化または過小平滑化の落とし穴を回避するのに役立ちます。
実際、フリードマン・ディアコニスの法則は、何らかのリスク尺度を最小限に抑えるように導出されています。 この導出方法は非常に一般的であり、同様のアプローチに従うストーンの法則のような同様の代替方法があります。 これらのルールはすべて導出および実装が簡単であるため、スタージェスのような古いルールが依然として使用されている理由はありません。
ただし、これらの方法はすべて、すべてのデータ範囲に対して一意のビン幅を想定しています。 もちろん、これは厳しすぎる制約です。十分に豊富なデータ セットには、データ セット内の詳細が平滑化されるか、適合が不十分になる領域が存在するためです。 このため、カーネル密度推定のような適応型手法を使用する方がはるかに優れています。 ラリー・ワッサーマン著「統計のすべて」の第 20 章に、素晴らしい議論が記載されています。
コルモゴロフ・スミルノフ検定の不適切性
Kolmogorov-Smirnov (KS) 検定は、サンプルの経験的分布関数を参照確率分布と比較するか、2 つのサンプル分布を比較するノンパラメトリック検定です。 データ範囲全体にわたる分布間の不一致に敏感です。 比較される統計量は、両方の分布の累積分布関数(cumulative distribution function, cdf)の差の最大値です。 もちろん cdf は完全なデータセットから取得されますが、多くの論文や、ヒストグラムからビン化されたデータを使用する商用ソフトウェアの実装さえも見てきました。 これは許容可能な近似値のように見えるかもしれませんが、実際には検定の検出力が大幅に低下し、データセットについて何の仮定も行わないノンパラメトリック検定が、結果がヒストグラムビニング方法に大きく依存する検定に変わってしまいます。
たとえば、2 つの分布からのデータを比較してみることができます。どちらも平均 0、分散 1 の正規分布で、それぞれから 100 個のサンプルが取得されます。このデータからシミュレーションを実行し、たとえば 95 パーセントの信頼レベルで KS p 値を計算し、偽陽性率を推定できます。経験的 CDF を使用してこの手順に従うと、fpr は約 5 パーセントになります (予想どおり)。ただし、ヒストグラムを使用すると、fpr は約 50 パーセントになります。
同様のテストを実行することもできますが、両方の分布の平均がゼロになるのではなく、片方が 0.5 に設定されます。今回は、フル データ KS は 95% CL で 80% の確率で帰無仮説を棄却しますが、ヒストグラムは 50% の確率で棄却します。前に述べたように、ヒストグラム ベースのテストの検出力は、フル データ セット テストよりもはるかに低くなります。
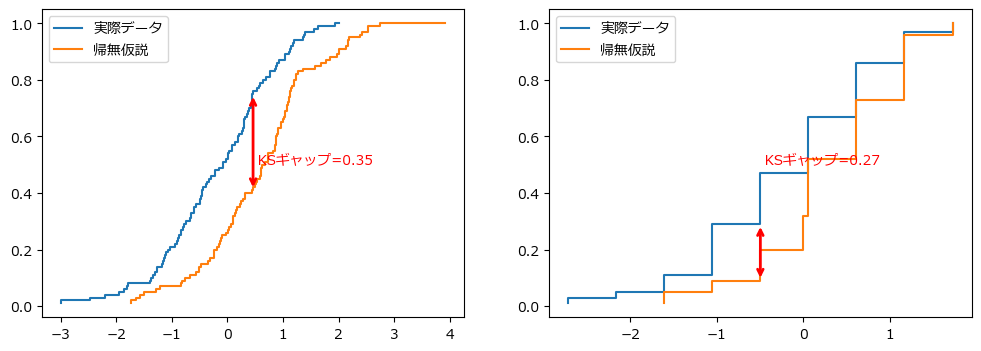
これらは、そうしたシミュレーションの 1 つの結果です。もちろん、これは非常に大まかな実験ですが、確率分布の特徴はヒストグラムよりも cdf の方がはるかに明確です。
分類方法の校正における課題
これはおそらく最も複雑な例です。 問題は次のようになります。分類の問題に直面したとき、多くの場合、ビジネスではクラスの予測 (バイナリの場合の A 対 B) だけでなく、各クラスの確率も必要になります。 典型的なシナリオは、信用リスクの評価です。 この場合、債務不履行の確率は通常非常に低く、非確率的な予測では、信用リスクがたとえば 40%、高いものの 50% 未満であるクレジット申請を区別できないため、最大値を使用して債務不履行ではないと分類されます。 事実上リスクのないアプリケーションからの事後 MAP ルール。 あるいは、デフォルト確率を使用して適切な金利を設定することもできます。
したがって、良好な分類子スコア結果 (AUC など) を得るために確率モデル (おそらく最も簡単なケースではロジスティック回帰、またはより一般的にはプラットのようなスケーリング手法) を作成しますが、その後、割り当てられた確率がどの程度正確であるかをテストする必要があります。 この最後のステップはキャリブレーションとして知られています。
キャリブレーションには、予測確率と実際の結果を比較して、予測確率が真の確率を反映していることを確認することが含まれます。 誤ったキャリブレーションは自信過剰な予測につながる可能性があり、リスクに敏感なアプリケーションでは有害です。
ただし、キャリブレーションにヒストグラムを使用すると、問題が発生する可能性があります。 同じビン内のすべてのイベントに同じ確率が割り当てられるため、ビン分割プロセスでは重大な情報損失が発生します。 これは直感的には正しいですが、arxiv:1909.10155 のように形式化することができます。 この論文では、ビニング方法がどのように真の誤差を過小評価し、その結果楽観的すぎる結果になりやすいかを示します。 ただし、繰り返しになりますが、私はこの方法が現実の生活 (商用ソフトウェア パッケージを含む) に適用されているのを見てきました。 この場合、解決策は前のケースほど単純ではありませんが、前述の論文ではこの問題を改善する方法が紹介されています。
このような場合には、別のアプローチもいくつかあります。 もちろん、ベイズ文献はこれらの問題を扱ってきました。 しかし、おそらく、頻度主義の観点から不確実性を定量化するための最良のアプローチは、Vovk らの等角予測法です。 (Journal of Machine Learning Research 9 (2008) 371-421)。
結論
ヒストグラムは適切に使用すれば強力なツールですが、単純なビニング方法を使用すると誤解を招く可能性があります。 スタージェスのルールは単純ですが、大規模なデータセットでは失敗することが多く、不適切なビニングにつながります。 フリードマン・ディアコニス規則または適応カーネル手法により、データ分布をより忠実に表現できます。 さらに、ビニングによって情報損失が生じるため、コルモゴロフ・スミルノフ検定の計算にはヒストグラムを使用しないでください。 最後に、分類法のキャリブレーションでは、誤ったキャリブレーションを避けるために、ヒストグラムに基づく方法よりもより洗練された技術を優先する必要があります。 これらのニュアンスを理解することは、正確なデータ分析とモデル評価にとって重要です。

